Valuation
It is somewhat inevitable that a discussion on credit options will require some explanation of their valuation. We can value credit options using a modified version of the Black Scholes Merton framework. Although I have no desire to reinvent the wheel here (and bore my audience to death) there are two perspectives one can take to understand the intuition of what the model is trying achieve.
Buyer: What payout do I expect to receive?
Seller: What is the cost of hedging my exposures?
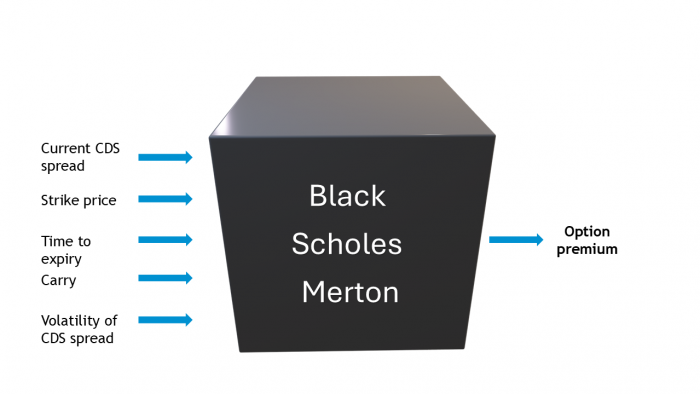
Visualising valuation
The following diagram conveys a sense of the key CDS option inputs, without getting bogged down in the formulas.
Quoting credit options
A stylised example of a ‘trader’s run’ might look as follows:
Underlying index: series XX
Current index price: 85 bps (i.e. the par spread)
Expiry date: 3 months
Strike Vol Payer premium Receiver premium
90 68% 35 47
95 69% 27 62
100 70% 21 71
The example shows that the premium quoted as a mid-market rate expressed in basis points. So if I were to buy a payer with a strike of 90 with a notional of 10m the cost would be an upfront premium of 35,000. If exercised the buyer would buy protection paying a fixed coupon of 100 bps p.a. As mentioned in the previous post, if the buyer were to exercise the option there will be an upfront adjustment typical of any non-option CDS.
Admittedly, I have oversimplified here – some of you will no doubt be shouting at the screen as I have not talked about the concept of the forward spread, which as is the case for all European-style option models, forms the basis of the premium calculation. We need to take yet another digression in the next post to talk about the PV01 and why it is not the same as the DV01.

